[ No 4 ]
IMAGE ENCRYPTION
5 image encryption methods based on chaotic maps
Programming
20 APRIL 2021
Sitemap
q-deformed logistic map
Chaotic logistic map
Cross-coupled chaotic map
Combined chaotic map
Chaotic standard and logistic map
Chaotic Maps
In the design of an encryption-decryption chaotic system, the key space for which valid keys are to be chosen should be precisely specified and avoid non-chaotic regions. In such a case, within the chaotic regime, the sensitivity to the parameters will guarantee that two orbits starting from the same initial point but with slightly different parameters will exponentially diverge.
Disclaimer: All 5 algorithms implemented have been amended to fit RGB images. Decryption methods are reflective of the encryption methods.
Image encryption using q-deformed logistic map
In this paper, the proposed encryption method is applied to 8-bit images in which a q-deformed logistic (chaotic) map is used based on the characteristics of sensitivity to the initial conditions and pseudo-randomness. Using a q-deformation of the map, we increase the size of the key space instead of using a high-dimensional chaotic map. It is worth mentioning that a low-dimensional chaotic map has several advantages, including easy implementation and parallel processes in the generation of chaotic sequences. The additional parameter, q, increases the level of security through the key space. By contrast, the topological entropy of the chaotic q-deformed logistic system can be computed with a fixed accuracy, which means that we can select the parametric region that best suits our purposes.

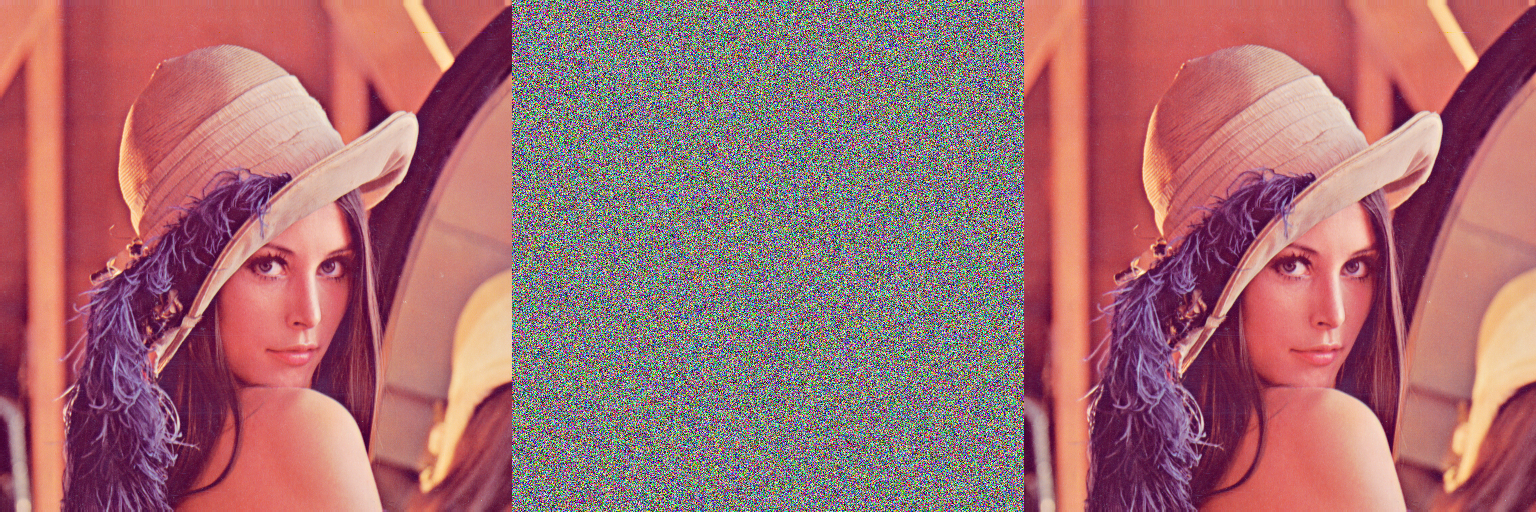
| Variables | Values |
|---|---|
| xn | 0.6871409815023363787389598655864 |
| yn | 0.4102339834686560271492794527148 |
| zn | 0.5182795675111749877927991292381 |
| a1 | 3.9538320032982445795255443954375 |
| a2 | 3.8102660350797150634605259256205 |
| a3 | 3.8481480146370818928858170693275 |
| q1 | 1.3676273505774996230854867462767 |
| q2 | -0.0249366189753303935106032440672 |
| q3 | 1.7291988783192659973053650901420 |
| n1 | 54751 |
| n2 | 84301 |
| n3 | 90817 |
Image encryption using chaotic logistic map
As chaotic maps have many fundamental properties such as ergodicity, mixing property and sensitivity to initial condition/system parameter and which can be considered analogous to some cryptographic properties of ideal ciphers such as confusion, diffusion, balance and avalanche property etc. In this communication, a new image encryption scheme is proposed based on chaotic logistic maps in order to meet the requirements of the secure image transfer. In the proposed encryption process, eight different types of operations are used to encrypt the pixels of an image and which operation will be used for a particular pixel is decided by the outcome of the second logistic map. Thus, the second chaotic map further increases the confusion in the relationship between the encrypted and its original image. To make the cipher more robust against any attack, after each encryption of a block of sixteen pixels, the secret key is modified.
| Group no. | Intervals of Y values | Operations for encryption/decryption |
|---|---|---|
| 1 | 0.10–0.13, 0.34–0.37, 0.58–0.62 | NOT operation, i.e. invert the bits of all three RGB bytes |
| 2 | 0.13–0.16, 0.37–0.40, 0.62–0.66 | R⊕K4, G⊕K5 and B⊕K6 |
| 3 | 0.16–0.19, 0.40–0.43, 0.66–0.70 | Encryption |
| ((R)10+(K4)10+(K5)10) mod 256, ((G)10+(K5)10+(K6)10) mod 256, ((B)10+(K6)10+(K4)10) mod 256 | ||
| Decryption | ||
| ((R)10+256−(K4)10−(K5)10), ((G)10+256−(K5)10−(K6)10), ((B)10+256−(K6)10−(K4)10) | ||
| 4 | 0.19–0.22, 0.43–0.46, 0.70–0.74 | Encryption |
| NOT(R⊕K4), NOT(G⊕K5), NOT(B⊕K6) | ||
| Decryption | ||
| (NOT(R))⊕K4, (NOT(G))⊕K5, (NOT(B))⊕K6 | ||
| 5 | 0.22–0.25, 0.46–0.49, 0.74–0.78 | Similar to Group 2 except that K7, K8 and K9 are used in lieu of K4, K5 and K6, respectively. |
| 6 | 0.25–0.28, 0.49–0.52, 0.78–0.82 | Similar to Group 3 except that K7, K8 and K9 are used in lieu of K4, K5 and K6, respectively. |
| 7 | 0.28–0.31, 0.52–0.55, 0.82–0.86 | Similar to Group 4 except that K7, K8 and K9 are used in lieu of K4, K5 and K6, respectively. |
| 8 | 0.31–0.34, 0.55–0.58, 0.86–0.90 | No operations are made on R,G and B bytes |
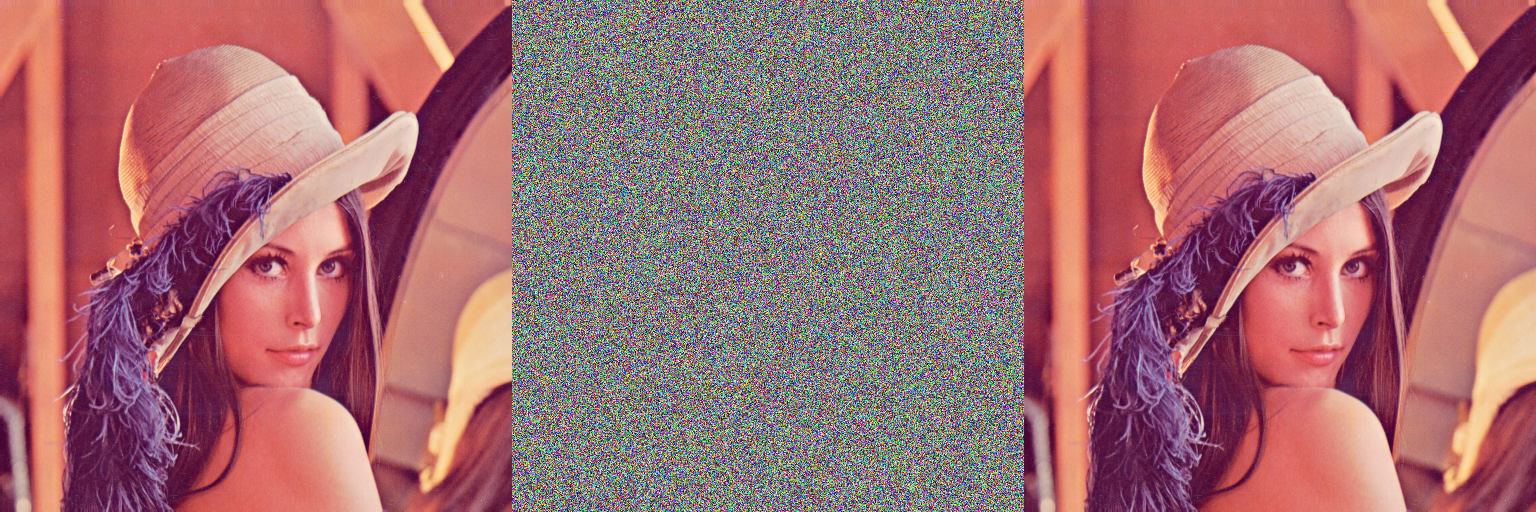
| Variables | Values |
|---|---|
| index1 | 4 |
| index2 | 6 |
| index3 | 0 |
| indexlist | [[0.8333333333333333, 0.8666666666666666], [0.7333333333333333, 0.7666666666666666], [0.6333333333333333, 0.6666666666666666], [0.7, 0.7333333333333333], [0.5666666666666667, 0.6], [0.16666666666666669, 0.2], [0.33333333333333337, 0.3666666666666667], [0.3666666666666667, 0.4], [0.4, 0.43333333333333335], [0.26666666666666666, 0.30000000000000004], [0.7666666666666666, 0.7999999999999999], [0.13333333333333333, 0.16666666666666669], [0.6666666666666666, 0.7], [0.1, 0.13333333333333333], [0.5, 0.5333333333333333], [0.5333333333333333, 0.5666666666666667], [0.7999999999999999, 0.8333333333333333], [0.8666666666666666, 0.9], [0.4666666666666667, 0.5], [0.30000000000000004, 0.33333333333333337], [0.2, 0.23333333333333334], [0.23333333333333334, 0.26666666666666666], [0.6, 0.6333333333333333], [0.43333333333333335, 0.4666666666666667]] |
| grouplist | [4, 5, 6, 6, 6, 3, 0, 1, 0, 3, 2, 3, 7, 5, 7, 4, 2, 1, 0, 5, 7, 4, 2, 1] |
| k | [‘1111’, ‘0110’, ‘1000’, ‘0111’, ‘0000’, ‘0010’, ‘0010’, ‘0010’, ‘0111’, ‘0001’, ‘0100’, ‘0101’, ‘0101’, ‘1100’, ‘1000’, ‘0111’, ‘1100’, ‘0111’, ‘0011’, ‘1001’] |
Multiple grayscale image encryption using cross-coupled chaotic maps
This paper proposes a newly developed multiple grayscale image encryption scheme using cross-coupling of two Piece-wise Linear Chaotic Maps (PWLCM). In this scheme, cross-coupled PWLCM systems are used to perform both the permutation and diffusion operation. The sorted iterated sequences of cross-coupled PWLCM systems are used to perform the row-column diffusion operation, whereas their corresponding indexed sequences are used to execute the row-column permutation operation. The cross-coupled chaotic map improves the discrete dynamics of chaos and avoids the weakness of using a single chaotic map for permutation-diffusion operation. The use of a cross-coupled chaotic map increases the difficulty of cryptanalysis of the cipher image because the cipher output is generated by the mixing of different chaotic orbits. In addition to this, the cross-coupling of a single type of chaotic map (PWLCM system) increases the software and hardware efficiency of the algorithm. As well as, the use of the PWLCM system increases the encryption speed of the algorithm. The proposed technique also uses the Secure Hash Algorithm SHA-256 to resist the algorithm against the known-plaintext attack and the chosen-plaintext attack.
The two important features for selecting any chaotic map in image encryption are “simplicity” and “ergodicity”. PWLCM is the map that offers simplicity and wider range of ergodicity.



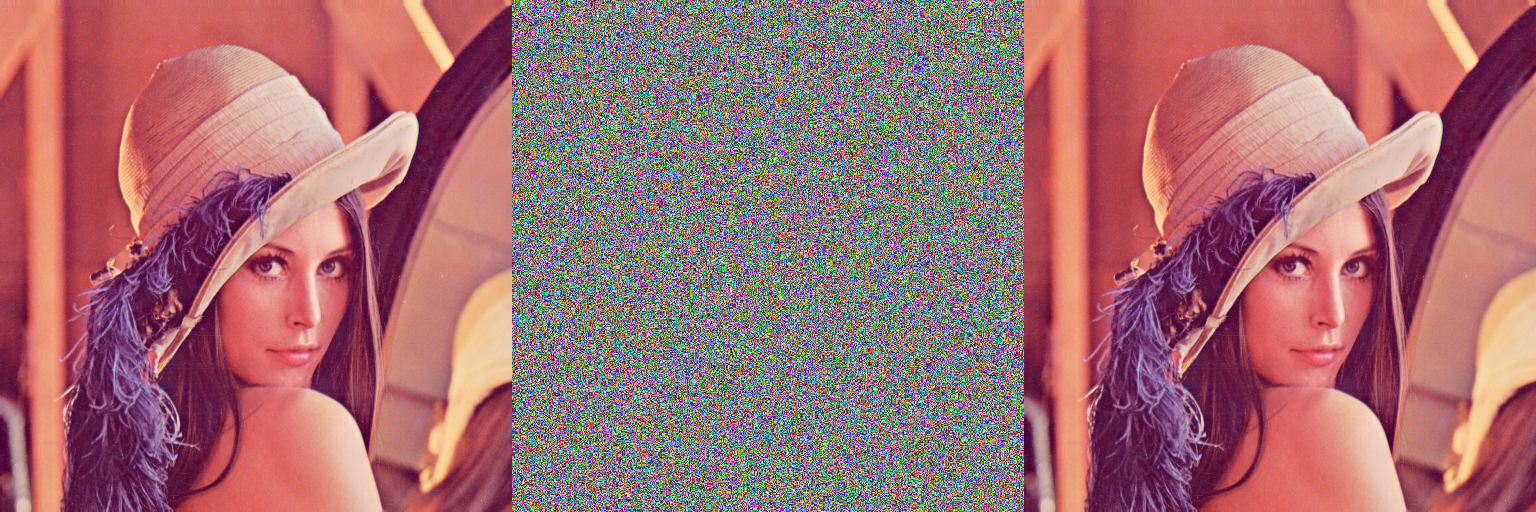
| Variables | Values |
|---|---|
| x0 | 0.2762535590204497 |
| xx | 0.3928896916940632 |
| y0 | 0.020024310395463152 |
| yx | 0.6365662408360173 |
| hsh | 56c85fdb591c89abbb61bdb631070202394d5fd5c144daff1303f413351b3a37 |
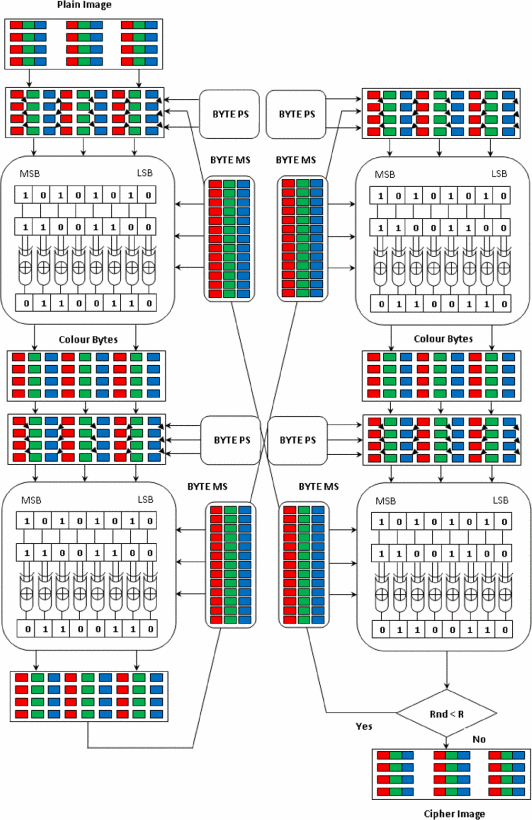
Colour byte scrambling technique for efficient image encryption based on combined chaotic map
In this paper, an image encryption scheme based on colour byte scrambling technique is proposed by using Logistic map and Ikeda map. The proposed scheme is using Logistic map for generating permutation sequence to shuffle the colour bytes (confusion) and Ikeda map is used for generating masking sequence to change the value of the colour bytes (diffusion) of the 24-bit colour image. The traditional scrambling techniques confusion and diffusion are applied continuously on the test image which leads to producing the cipher image which has good confusion and diffusion properties. In this scheme, the Logistic map is one dimensional which is simple and efficient and used for the generation of permutation sequences for achieving confusion. The two-dimensional Ikeda map is used for the generation of masking sequences for achieving diffusion.
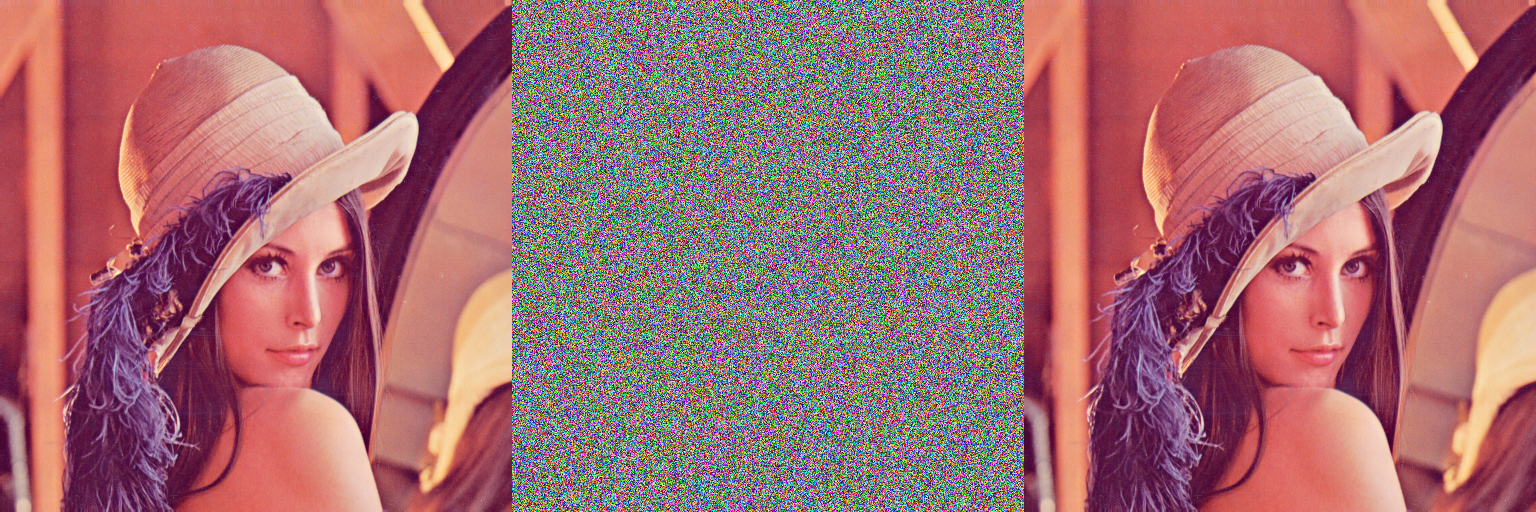
| Variables | Values |
|---|---|
| r1 | 3.6417036301636764861200390441809 |
| r2 | 3.7156486229407827970305788767291 |
| r3 | 3.5273648853144021764194349088939 |
| r4 | 3.9557898564534217378252378694015 |
| x1 | 0.2269487821938834803958684460667 |
| x2 | 0.3226240330364515962457971909316 |
| x3 | 0.8572765495553988923660426735296 |
| x4 | 0.6886448160968399179182597436011 |
| y1 | 0.5760091308256071185311952831398 |
| y2 | 0.6593374068771247209497232688591 |
| miu | 0.8962150996380580103561896976316 |
Modified substitution–diffusion image cipher using chaotic standard and logistic maps
In this paper, we propose a new loss-less symmetric image cipher based on the widely used substitution–diffusion architecture which utilizes the chaotic 2D standard map and 1D logistic map. It is specifically designed for the coloured images, which are 3D arrays of data streams. The initial condition, system parameter of the chaotic standard map and number of iterations together constitute the secret key of the algorithm. The proposed algorithm comprises of four rounds: two for the substitution and two for the diffusion. The first round of substitution/confusion is achieved with the help of intermediate XORing keys calculated from the secret key. Then two rounds of diffusion namely the horizontal and vertical diffusions are completed by mixing the properties of horizontally and vertically adjacent pixels, respectively. In the fourth round, a robust substitution/confusion is accomplished by generating an intermediate chaotic key stream (CKS) image in a novel manner with the help of chaotic standard and logistic maps.
Modifications are made to make it more robust against two more cryptanalytic attacks. (Structural flaws such as known plain text attacks)



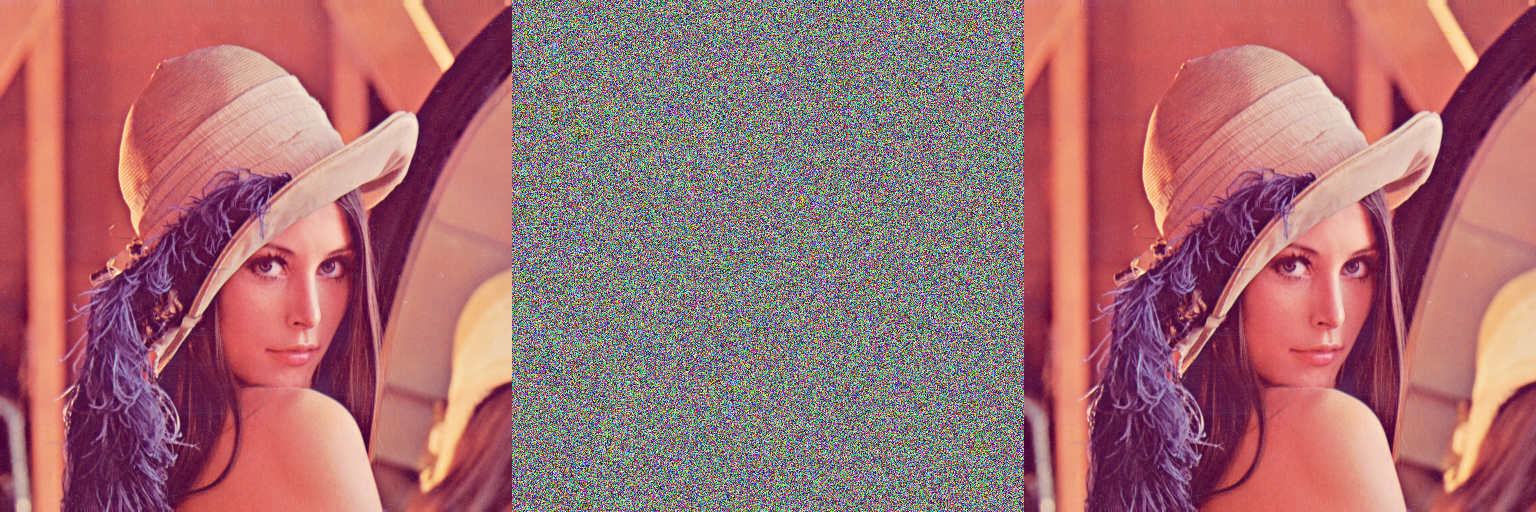
| Variables | Values |
|---|---|
| xn | 2.5186675676171912 |
| yn | 5.792031495262999 |
| K | 704.2434846927956 |
| N | 840 |
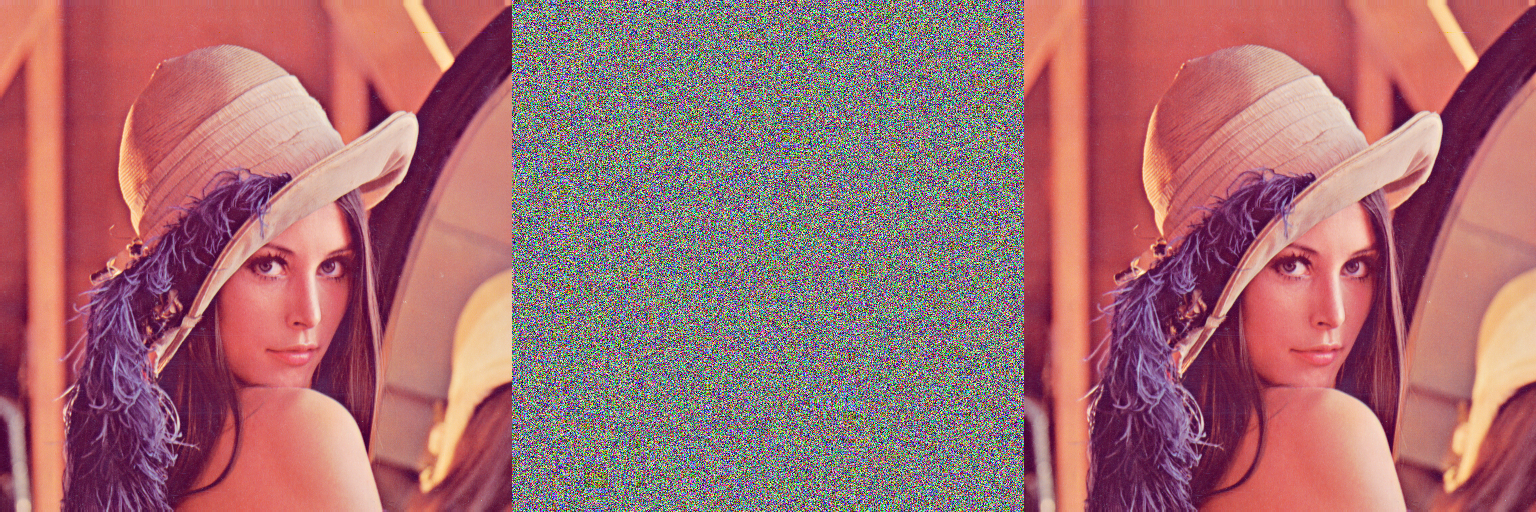
| Variables | Values |
|---|---|
| xn | 5.373068425055542 |
| yn | 5.101480085089893 |
| K | 483.88949085953874 |
| N | 141 |
by Aaron Ti